Research
Research Areas
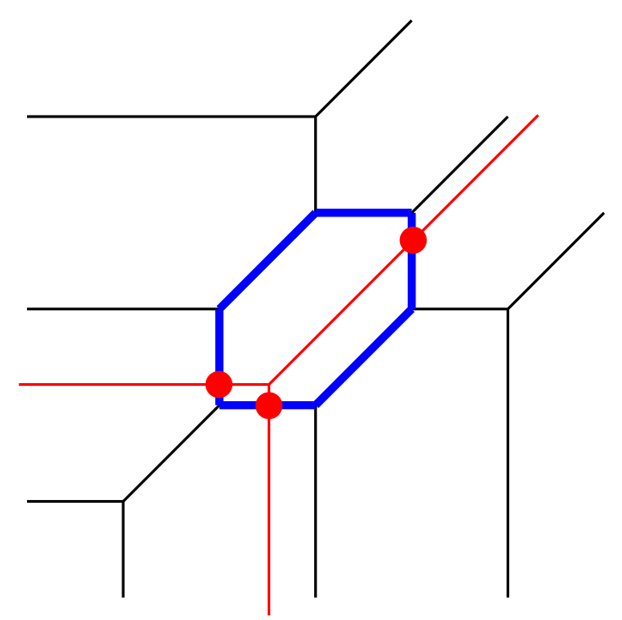
A tropical elliptic curve, genus 1 (blue), degree 1 (red)
Tropical Geometry
Tropical geometry studies piecewise-linear structures that arise in many seemingly unconnected areas. These so-called tropical varieties appear as combinatorial shadows of algebraic varieties in mathematics, as spaces of phylogenetic trees in biology, as indifference-price loci in economics, and as linear regions of ReLU networks in machine learning. The widespread presence of tropical varieties gives tropical geometry many applications, as well as a rich collection of tools. My research in tropical geometry is mainly concerned with explicit computations, such as the design and implementation of new algorithms.
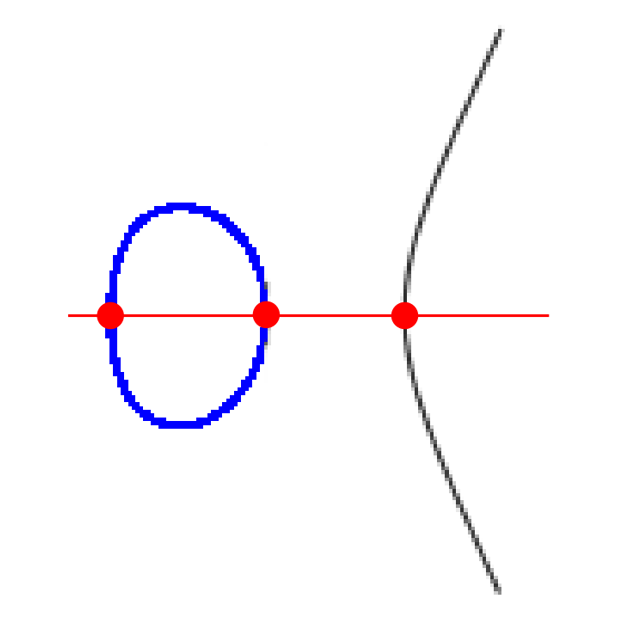
An algebraic elliptic curve, genus 1 (blue), degree 3 (red)
Algebraic geometry
Algebraic geometry studies geometric objects defined by polynomial equations and the algebraic structures that govern them. It provides a unifying language for problems across mathematics, connecting geometry, algebra, number theory, and combinatorics through concepts such as varieties, morphisms, and moduli spaces. My research in algebraic geometry focuses on explicit computations and on the application of tropical techniques
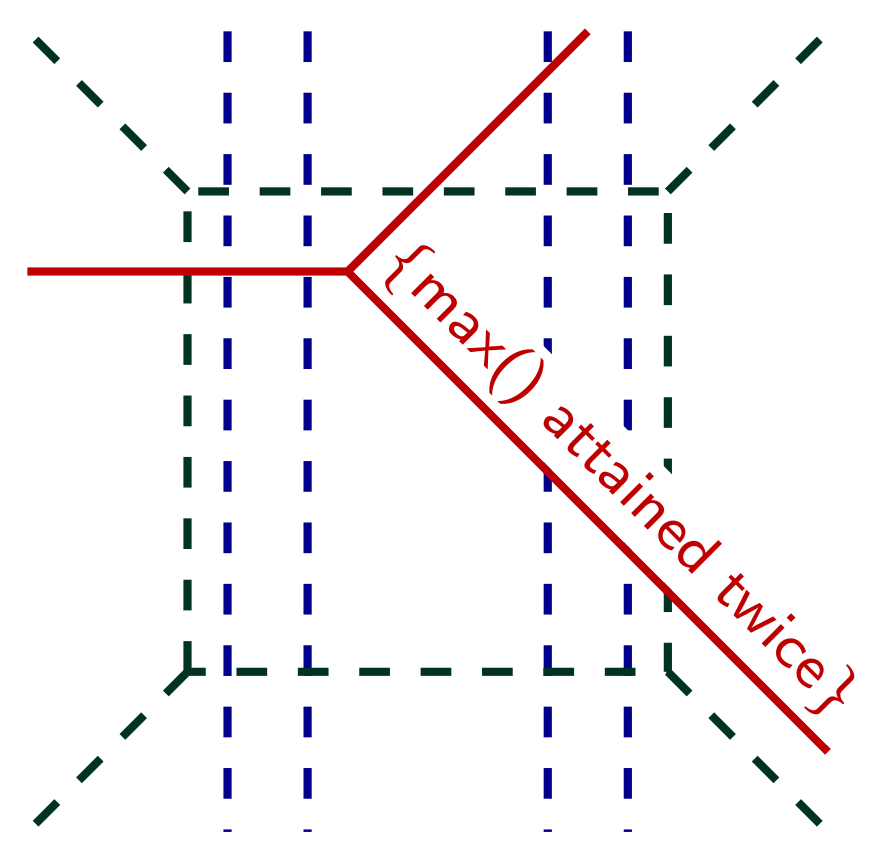
A maxout neural network from the lens of tropical geometry
Machine learning
Machine learning has become a central tool in many real-world applications, yet our theoretical understanding of both its capabilities and its limitations remains limited. Recent pure-mathematical approaches, such as neuroalgebraic geometry and singular learning theory, offer new perspectives on long-standing open problems in the field. My research in machine learning focuses on understanding the structure of existing models and on designing new models using tools from tropical and non-Archimedean geometry.
Research Topics
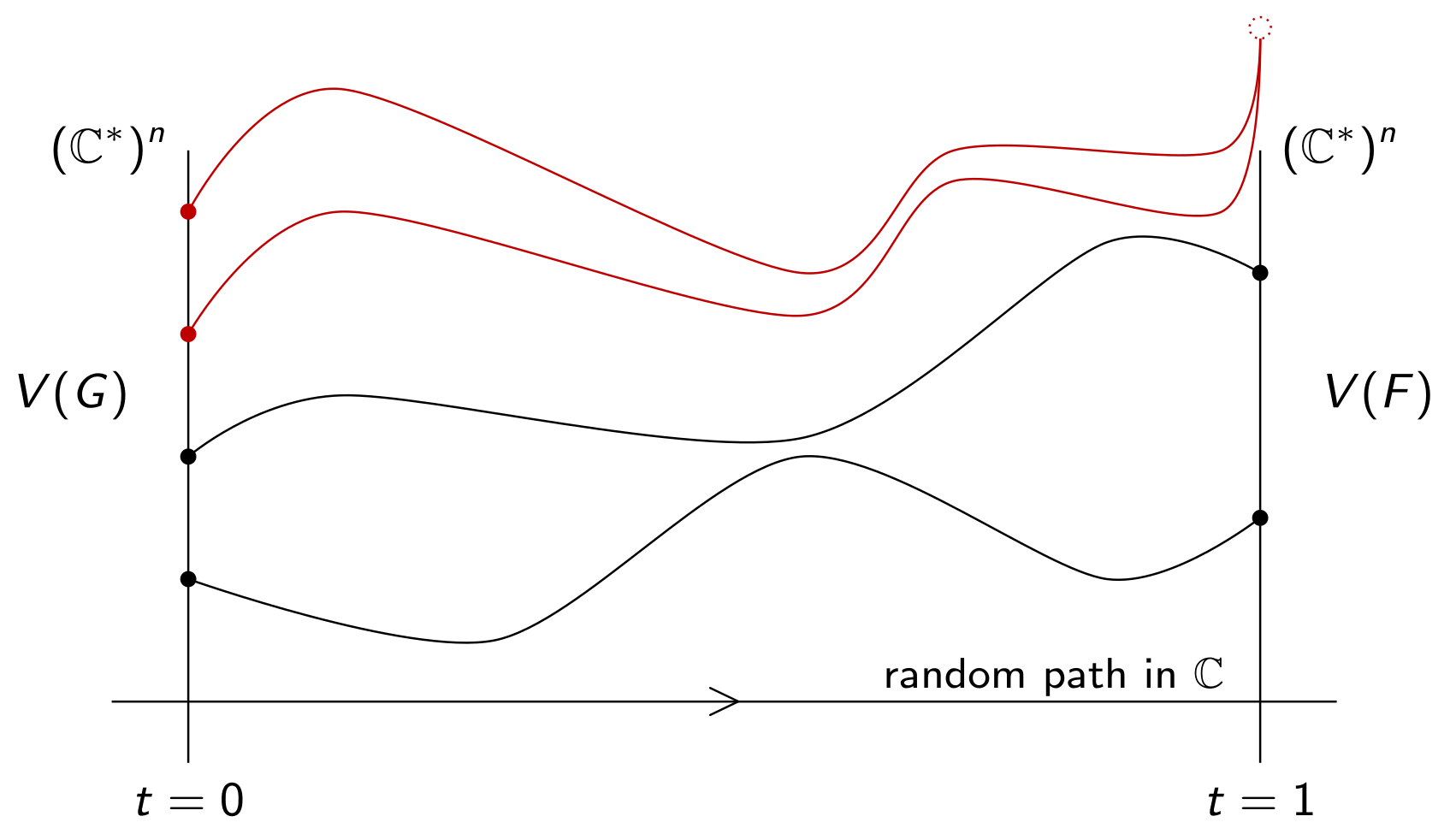
Solving polynomial system via homotopy continuation
Polynomial system solving
Polynomial systems are ubiquitous in the sciences. They describe the movement of planets, the kinematics of robotic mechanisms, the dynamics of chemical reactions, and the behaviour of coupled oscillators. Solving such systems efficiently is a fundamental problem with many applications. My research explores the use of tropical geometry to develop new techniques for polynomial system solving.
Gradient descent over the 2-adic numbers via Berkovich analytification
Nonarchemedian optimisation
Data plays an important role in the real world, but unlike the data typically studied in statistics, real-world data rarely consist of points in Euclidean space. Instead, they are often multifaceted and exhibit a clear hierarchical structure, such as people in a social network, videos on a video platform, or sequences in a genetic database. My research explores the use of tropical geometry to develop new techniques for hierarchical data analysis.