Papers

Publications and Preprints

(articles without arXiv links are open access; see below for a description of selected papers)

I. Holt, Y. Ren: Generic root counts of tropically transverse systems. arXiv:2311.18018.
P. A. Helminck, Y. Ren: Generic root counts and flatness in tropical geometry. arXiv:2206.07838.
Y. Ren: On intersections and stable intersections of tropical hypersurfaces. To appear in Algebraic Combinatorics. arXiv:2302.12335.
H. Gangl, Z. Urbancic: Hands on Tropical Geometry. Computeralgebra Rundbrief 72 (2023). arXiv:2304.10130.
D. Bendle, J. Boehm, Y. Ren, B. Schroeter: Massively parallel computation of tropical varieties, their positive part, and tropical Grassmannians. Journal of Symbolic Computation. doi:10.1016/j.jsc.2023.102224.
G. Montufar, Y. Ren, L. Zhang: Sharp bounds for the number of regions of maxout networks and vertices of Minkowski sums. SIAM Journal for Applied Algebra and Geometry 6 (2022), no. 4, 618-649. doi:10.1137/21M1413699.
P. Görlach, Y. Ren, L. Zhang: Computing zero-dimensional tropical varieties via projections. Computational Complexity 31 (2022), article no 5. doi:10.1007/s00037-022-00222-9.
P. Görlach, Y. Ren, J. Sommars: Detecting tropical defects of polynomial equations. Journal of Algebraic Combinatorics 53 (2021), 31-47. doi:10.1007/s10801-019-00916-4.
N. Kaihnsa, Y. Ren, M. Safey El Din, J. W. R. Martini: Cooperativity, Absolute Interaction, and Algebraic Optimization. Journal of Mathematical Biology 81 (2020), 1169-1191. doi.org:10.1007/s00285-020-01540-8.
T. Markwig, Y. Ren: Computing tropical varieties over fields with valuation. Foundations of Computational Mathematics 20 (2020), 783-800. doi:10.1007/s10208-019-09430-2.
J. Böhm, S. Keicher, Y. Ren: Computing GIT-fans with symmetry and the Mori chamber decomposition of M06. Mathematics of Computation 89 (2020), 3003-3021. doi:10.1090/mcom/3546.
M. Hahn, H. Markwig, Y. Ren, I. Tyomkin: Tropicalized quartics and canonical embeddings for tropical curves of genus 3. International Mathematics Research Notices (2019), rnz084. doi:10.1093/imrn/rnz084. arXiv:1802.02440.
A. Jensen, Y. Ren, H. Schoenemann: The gfanlib interace in Singular and its applications. Journal of Software for Algebra and Geometry 9 (2019), 81-87. doi:10.2140/jsag.2019.9.81.
T. O. Celik, A. Kulkarni, Y. Ren, M. Sayyary: Tritangents and their space sextics. Journal of Algebra 538 (2019), 290-311. doi:10.1016/j.jalgebra.2019.07.037. arXiv:1805.11702.
Y. Ren, J. W. R. Martini, J. Torres: Decoupled molecules with binding polynomials of bidegree (n,2). Journal of Mathematical Biology 78 (2019), no. 4, 879-898. doi:0.1007/s00285-018-1295-x.
A. Kulkarni, Y. Ren, M. Sayyary, B. Sturmfels: Real space sextics and their tritangents. Proceedings of the ISSAC 2018 (2018), 247-254. doi:10.1145/3208976.3208977. arXiv:1712.06274.
T. Hofmann, Y. Ren: Computing tropical points and tropical links. Discrete Computational Geometry 60 (2018), no. 3, 627-645. doi:10.1007/s00454-018-0023-z.
R. Epure, H. Schönemann, Y. Ren: The polymake interface in Singular and its applications. Lecture Notes in Computer Science 10490 (2017), 109-117. doi:10.1007/978-3-319-66320-3_9.
T. Markwig, Y. Ren: Gröbner fans of x-homogeneous ideals in R[[t]][x]. Journal of Symbolic Computation 83 (2017), 315-341. doi:10.1016/j.jsc.2016.11.016. arXiv:1512.02662.
T. Markwig, Y. Ren, O. Wienand: Standard bases in mixed power series and polynomial rings over rings. Journal of Symbolic Computation 79 (2017), no. 1, 119-139. doi:10.1016/j.jsc.2016.08.009. arXiv:1509.07528.
J. Böhm, W. Decker, S. Keicher, Y. Ren: Current challenges in developing open source computer algebra systems. Lecture Notes in Computer Science 9582 (2016), 3-24. doi:10.1007/978-3-319-32859-1_1. arXiv:1702.06912.
M. Marais, Y. Ren: Mora's holy grail: Algorithms for computing in localizations at prime ideals. International Journal of Algebra and Computation 25 (2015), no. 7, 1125-1143. doi:10.1142/S0218196715500332. arXiv:1504.01648.
M. Cuntz, Y. Ren, G. Trautmann: Strongly symmetric smooth toric varieties. Kyoto Journal of Mathematics 52 (2012), no. 3, 597-620. doi:10.1215/21562261-1625208. arXiv:1108.1886.

Generic Root counts and flatness in tropical geometry

In this paper, we use tropical geometry to compute generic root counts of families of polynomial systems. This is done in three steps:

Study when a generic root count can be expressed as a tropical intersection number (this is a generalization of Bernstein’s Theorem A+B)
Explore ways to modify square polynomial system into a desired combinatorial shape
Find ways to compute the resulting tropical intersection number

Our main examples are families with fixed polynomial support [KK12], and steady state equations of chemical reaction networks [Dic16].

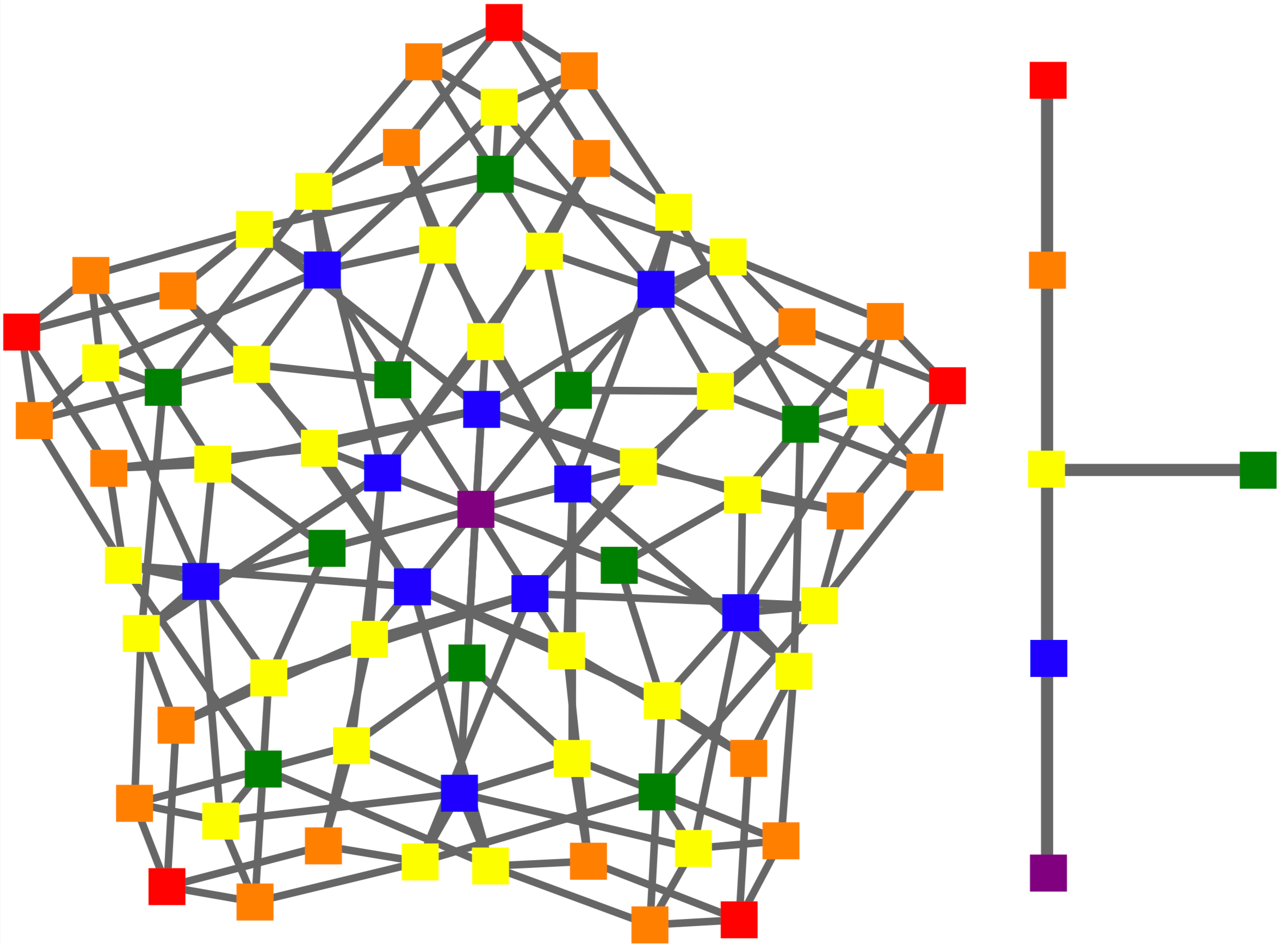
Sharp bounds for the number of regions of maxout networks and vertices of Minkowski sums

In this paper, we construct an upper bound for the possible number of linear regions of maxout networks with a fixed architecture, which can be regarded as a measure for their expressitivity. Our bounds are sharp for shallow networks, and asymptotically sharp for deep networks.
In our work, we rely on the correspondence between linear regions of maxout shallow maxout networks, regions of tropical hypersurfaces arrangements, and upper vertices of Minkowski sums of polytopes (see picture).

Tropicalized quartics and canonical embeddings for tropical curves of genus 3

Brodsky, Joswig, Morrison and Sturmfels Urban Base Executiveshowed that not all abstract tropical curves of genus three can be realized as a tropicalization of a quartic in the euclidean plane. In this article, we focus on the interior of the maximal cones in the moduli space and classify all curves which can be realized as a faithful tropicalization in a tropical plane. Reflecting the algebro-geometric world, we show that these are exactly those which are not realizably hyperelliptic.
Our approach is constructive: For any not realizably hyperelliptic curve, we explicitly construct a realizable model of the tropical plane and a faithfully tropicalized quartic in it. These constructions rely on modifications resp. tropical refinements. Conversely, we prove that any realizably hyperelliptic curve cannot be embedded in such a fashion. For that, we rely on the theory of tropical divisors and embeddings from linear systems, and recent advances in the realizability of sections of the tropical canonical divisor.

Decoupled molecules with binding polynomials of bidegree (n,2)

In this paper, we study an interesting class of parametrized system of polynomial equations arising from biochemistry, using algebraic geometry and computer algebra software. In particular, we determine its generic number of solutions.

In biology and chemistry, many systems are centered around a process where one substance binds to multiple sites of another object, such as oxygen binding to the four sites of hemoglobin. In this case, oxygen is referred to as a ligand while hemoglobin is called the target molecule. The binding polynomial is the denominator of the rational function describing the average number of occupied binding sites in relation to the ligand activity. It describes the binding behaviour of the system.

In the Henderson-Hasselbalch-Modell, target molecules are characterized by binding energies on the sites and interaction energies between the sites. The binding polynomial, or rather its coefficients, are given by a square system of polynomials equations in the binding and interaction energies.

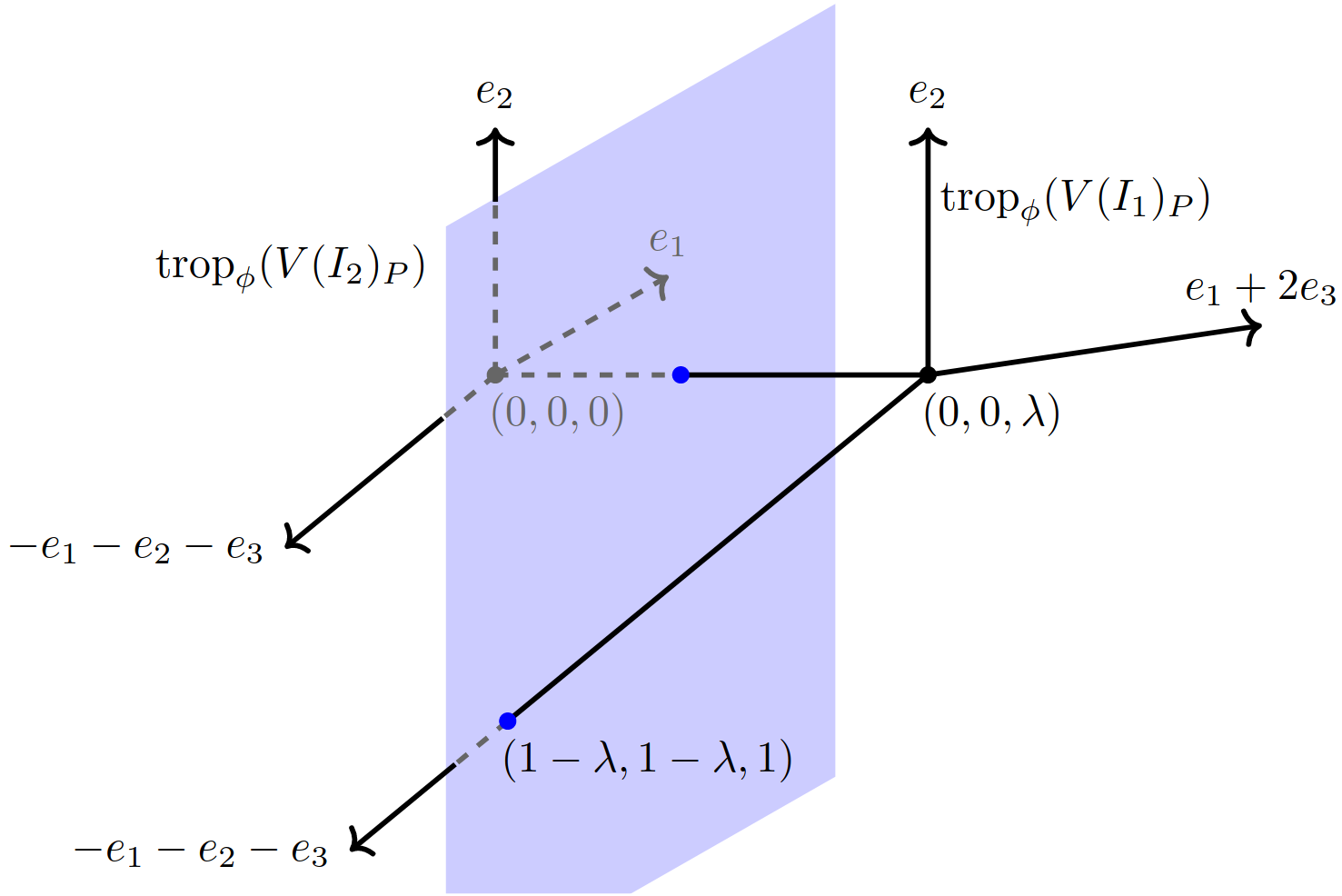
Computing tropical Points and tropical links

In this paper, we introduce a simple yet novel approach for computing non-trivial points on and codimension-one links of tropical varieties. The algorithm relies on bread-and-butter techniques in computer algebra, the heart being triangular decomposition and Newton polygons methods.

All algorithms are implemented in the Singular library tropicalNewton.lib and are publicly available as part of the official Singular distribution. They currently represent the fastest way for computing tropical varieties.

Computing tropical varieties over fields with valuation

In this paper, we show how tropical varieties over arbitrary fields with valuation can be computed using well-established standard bases techniques. Generalizing a known trick for the field of Puiseux series, we explain how the valuation can be emulated using an auxiliary variable. Doing so, we also obtain an alternative algorithm for computing so-called tropical Gröbner Bases as introduced by Chan and Maclagan.

All algorithms are implemented in the Singular library tropical.lib and are publicly available as part of the official Singular distribution.

Computing GIT-fans with symmetry and the Mori chamber decomposition of M06

In this paper, we propose an algorithm for computing the GIT-fan for torus actions on affine varieties with residual symmetries. The algorithm combines computational techniques from commutative algebra, convex geometry and group theory. We use our algorithm to compute the Mori chamber decomposition in the moving cone of the Deligne-Mumford compactification M06 of the moduli space of 6-pointed stable curves of genus zero.

All algorithms are implemented in the Singular library gitfan.lib and are publicly available as part of the official Singular distribution. Data on the GIT-Fan of M06 can be found on the website of the first author.